Урок 32. Работа на тренажере Логика К.Ю. Полякова

Дата проведения занятия  8а1 30.12.25

Дата проведения занятия  8а2 29.12.25

Дата проведения занятия  8б   29.12.25

Логика

тренажер для изучения логических элементов

Этот тренажер с сайта К.Ю. Полякова

Что это такое?

Тренажер «Логика» предназначен для проведения практических занятий по теме «Математическая логика» в игровой форме. Подобная игра была ранее написана для компьютеров «Ямаха» (программисты П. Меняйло и М. Щекочихин). Оригинал программы вместе с имитатором MSX-компьютера можно скачать здесь (спасибо Михаилу Бондаревскому).

Программа работает под управлением операционных систем линейки Windows 95/98/NT/2000/XP/2003 на любых современных компьютерах. После распаковки архива она находится в работоспособном состоянии и не требует никаких дополнительных настроек.

Правила игры

Задача заключается в том, чтобы последовательно передавать кристалл с верхней площадки на нижнюю. Подавая ток на вход механизмов в правой части схемы, можно выдвигать площадки на пути кристалла. Если на входе механизма нет тока, площадка убирается.

Для управления механизмами используют выключатели в левой части поля. Их состояние изменяется щелчком мыши. Если выключатель включен, по цепи идет ток и поступает на логические схемы, включенные в эту цепь (средняя часть поля). Логические схемы преобразуют входные сигналы по следующим правилам:

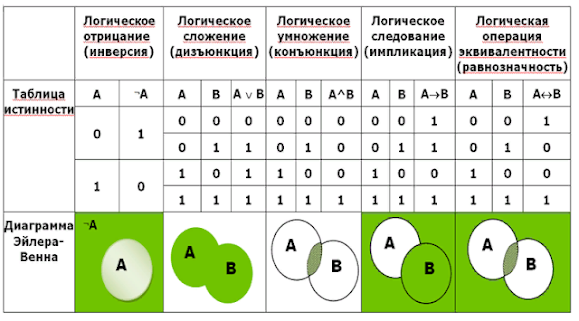
• схема НЕ: на выходе будет ток (сигнал 1), если на входе тока нет (сигнал 0), и наоборот;
• схема И: на выходе будет 1, если на обоих входах 1;
• схема ИЛИ: на выходе будет 1, если хотя бы на одном входе 1;
• схема XOR (исключающее ИЛИ): на выходе будет 1, если только на одном входе 1;
• схема импликация (1—>2): на выходе будет 0, если на первом входе 1, а на втором — 0; иначе на выходе 1;
• схема эквивалентность (<—>): на выходе будет 1, если оба входа равны; иначе на выходе 0.

Кристалл нельзя передавать сразу через несколько «пролетов» — в этом случае он разбивается и приходится начинать уровень заново. Кроме того, у вас есть только 5 кристаллов на всю игру, если вы разобьете их все, задание считается невыполненным.

Игра состоит из 10 уровней. Если вы сможете пройти все уровни, сохранив хотя бы один кристалл и наберете больше нуля очков, вы увидите картинку.

Задание на ПК

1. Скачать файл logic.zip на свой ПК

2. Распаковать файл с помощью программы 7-zip

3. Запустить файл logic.exe, выполнить задание

Урок 31. Преобразование логических выражений. Использование диаграмм Эйлера-Венна

Дата проведения занятия  8а1 25.12.25

Дата проведения занятия  8а2 24.12.25

Дата проведения занятия  8б   23.12.25

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

Выполнить Задание-3 на ПК

Домашнего задания нет

Урок 30. Преобразование логических выражений

Дата проведения занятия  8а1 23.12.25

Дата проведения занятия  8а2 22.12.25

Дата проведения занятия  8б   22.12.25

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

Выполнить Задание-2 на ПК

Домашнее задание
Закончить выполнение задания, начатого в классе, не позднее 22.00 час  23.12.25

Урок 29. Законы алгебры логики

Дата проведения занятия  8а1 18.12.25

Дата проведения занятия  8а2 17.12.25

Дата проведения занятия  8б   16.12.25

Законы алгебры логики

Рассматриваем свойства логических операций, с помощью которых делают  преобразование логических выражений

1.       ØØ  AºA                              2.       Ø (A&B) ºØA Ú ØB

3.       Ø (AÚB) ºØA & ØB              4.       Ø (A®B) ºA & ØB

5.       (A®B) ºØA Ú B                  6.       (A«B) º(A&B) Ú(ØA & ØB) º (ØA Ú B) & (A Ú ØB)

7.       A & (AÚB) ºA                     8.       A Ú A&B ºA

9.       ØA & (AÚB) º ØA & B      10.    A Ú ØA&B ºAÚB

11.    Законы коммутативности

A&BºB&A

AÚBºBÚA

12.    Законы ассоциативности

(AÚB)ÚC º AÚ(BÚC)

(A&B)&Cº A&(B&C)

13.    Законы повторения

AÚA º A

A&A º A

14.    Законы дистрибутивности

A&(BÚC) º (A&B) Ú(A&C)

AÚ (B&C) º (AÚB) & (AÚC) 

15.    AÚ1º1; A&1º A;   ØAÚ A º1

16.    A&0º 0;               ØA & A º0

Работа в классе

Ребята из одного класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Легенда №17», 11 человек – фильм «Сталинград»,  6 смотрели и «Легенда № 17», и «Сталинград». Нарисуйте в тетрадях диаграммы Эйлера-Венна и запишите эти  логические высказывания с помощью логических переменных. В этом файле вычислите, сколько человек посмотрели фильм «Легенда №17» или фильм «Сталинград»

Домашнее задание:

Обозначение операции ИЛИ  - |

Обозначение операции И  - &

Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:

  шахматы | теннис  7770
  теннис            5500
  шахматы & теннис  1000

Сколько страниц будет найдено по запросу

  шахматы ?

Урок 28. Вычисление значений логических выражений. Таблицы истинности

Дата проведения занятия  8а1 16.12.25

Дата проведения занятия  8а2 15.12.25

Дата проведения занятия  8б   15.12.25

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

Выполнить Задание-1 на ПК, диаграммы Эйлера-Венна нарисовать в тетради

Домашнее задание
1. Выучить таблицы истинности и диаграммы Эйлера-Венна для операций: И, ИЛИ, НЕ
2. Построить таблицы истинности:

а) F=¬(¬D ⋀ ¬E) ∨ ¬ E 

б) D=(A ∧ ¬C) ∨ ( ¬B ∧ ¬C)

Урок 27. Построение таблиц истинности для сложных логических выражений

Дата проведения занятия  8а1 11.12.25

Дата проведения занятия  8а2 10.12.25

Дата проведения занятия  8б   09.12.25

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

С помощью таблиц истинности можно выяснить, каково значение логического выражения при определенном значении переменных, входящих в него. На уроке смотрим презентацию  Таблицы истинности слайд 4, записываем алгоритм построения таблицы истинности. После этого строим таблицы истинности

A= (C ⋀ D) ∨ ¬ C

С=(А ∨ В) ⋀ ¬ В

B= ¬ (E ∨ F) ⋀ (¬E ∨ F)

F= А ⋀( ¬ В ∨ ¬ С)

Домашнее задание

1. Выучить таблицы истинности  и диаграммы Эйлера-Венна для операций: И, ИЛИ, НЕ

2. Построить таблицы истинности:

С=А ∨ А ⋀ В

D1 = A v (B & C)

D2 = (A v B) & (A v C)

Урок 26. Сложные высказывания. Диаграммы Эйлера-Венна

Дата проведения занятия  8а1 09.12.25

Дата проведения занятия  8а2 08.12.25

Дата проведения занятия  8б   08.12.25

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций.

Логические операции (в порядке убывания приоритета):

• инверсия (логическое отрицание, NOT),
• конъюнкция (логическое умножение, AND) ,
• дизъюнкция (логическое сложение, OR)
• импликация (следование) не проходим в 8 классе
• эквивалентность (равнозначность) не проходим в 8 классе

Смотрим презентацию Логические операции и логические выражения 
Повторяем логические операции, изучаем диаграммы Эйлера-Венна на слайдах с 3 по 7.
Решаем задачу с помощью диаграмм Эйлера-Венна на слайдах с 8 по 12

Домашнее задание

Выучить таблицы истинности  и диаграммы Эйлера-Венна для операций : И, ИЛИ, НЕ

Решить задачи со слайдов 27, 28, 29

Урок 25. Сложные высказывания. Логические операции

Дата проведения занятия  8а1 04.12.25

Дата проведения занятия  8а2 03.12.25

Дата проведения занятия  8б   02.12.25

2.11.1815 - день рождения Дж.Буля

Для тех, кто пропустил урок - ссылка на учебник Босовой Л.Л. , параграф 1.3

Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций.

Логические операции (в порядке убывания приоритета):

• инверсия (логическое отрицание, NOT),
• конъюнкция (логическое умножение, AND) ,
• дизъюнкция (логическое сложение, OR)
• импликация (следование) не проходим в 8 классе
• эквивалентность (равнозначность) не проходим в 8 классе

Смотрим презентацию Высказывания и логические связки слайды с 7 по 19 и строим таблицы истинности для инверсии, конъюнкции, дизъюнкции

Домашнее задание

Выучить таблицы истинности для операций : И, ИЛИ, НЕ